Introdução à Eletrônica - Resistores

Os resistores desempenham um papel fundamental na eletrônica. Esse tipo de componente elétrico é um dos mais simples de se entender, e seu correto entendimento é essencial para quem quer se aprofundar mais na área da eletrônica.

Dentro de um circuito elétrico, os resistores são os responsáveis por, como o nome sugere, criar uma resistência para a passagem de corrente. Nos esquemáticos de circuitos, os resistores são representados por um padrão em zigue-zague, conforme mostrado na figura abaixo. R1 representa um resistor de 1kΩ.

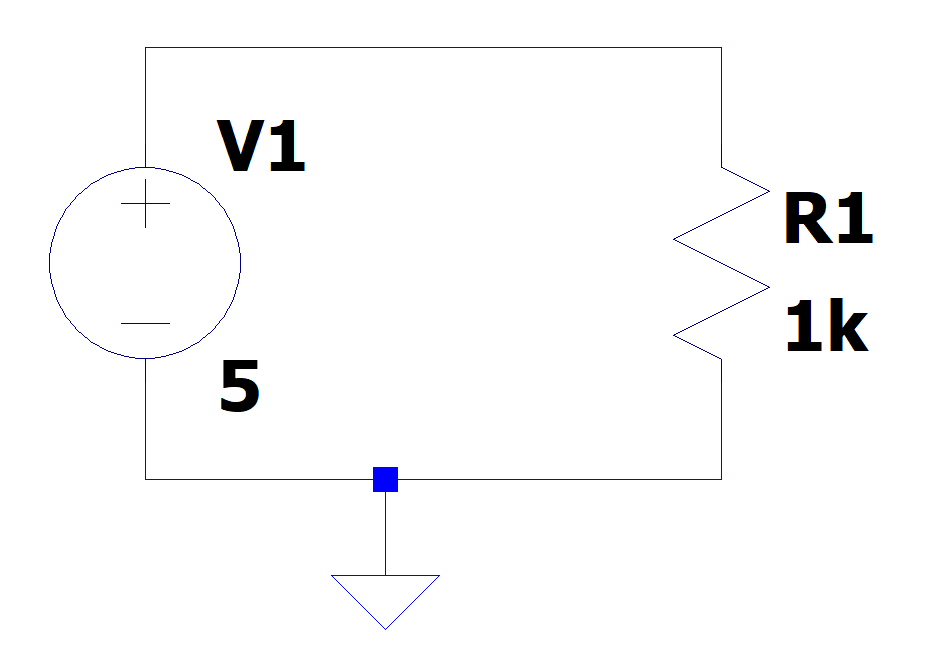
As fórmulas que explicam matematicamente o funcionamento dos resistores são chamadas Leis de Ohm.

Leis de Ohm

1° Lei de Ohm

A primeira lei de Ohm aborda a relação entre tensão, resistência e corrente. Conforme essa lei, a corrente que passa por um resistor é diretamente proporcional à tensão aplicada nos seus terminais. Ou seja, caso o dobro de tensão fosse aplicada, o dobro da corrente passaria pelo componente. A principal fórmula para entender essa relação é

Em que R representa a resistência elétrica, U representa a tensão aplicada e I a corrente gerada. Outras variações dessa mesma equação são

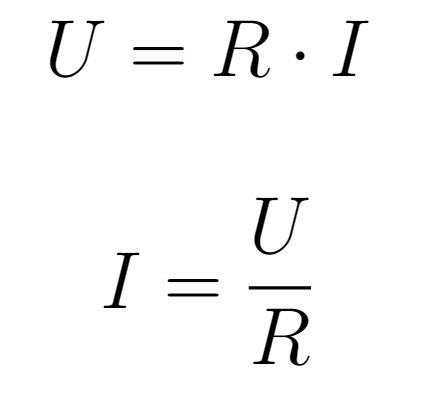
Essa equação assume que os resistores tem comportamento linear. Nesse contexto, o valor da resistência elétrica atua como um fator de proporção entre tensão e corrente.

Por exemplo, aplicar 5V em um resistor de 1Ω irá gerar

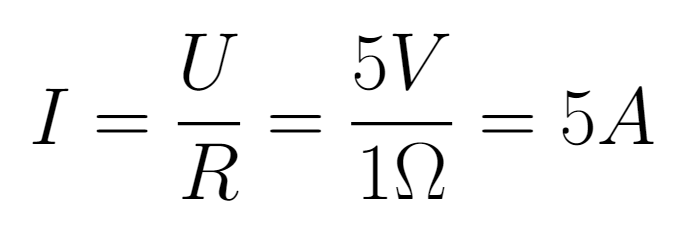
O fator de multiplicação entre tensão e corrente é de 1, pois 5V geram 5A. Já ao aplicar a mesma tensão em um resistor de 10Ω, a corrente gerada será

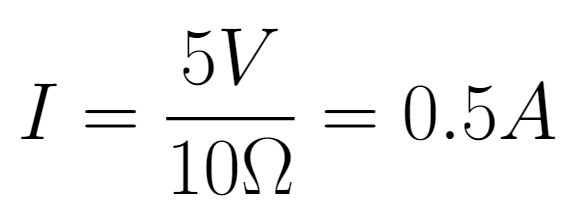
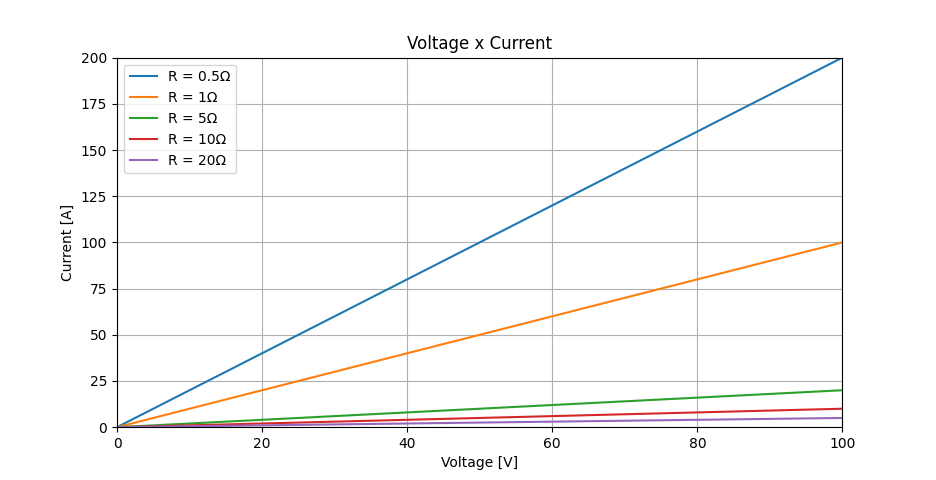
Agora, o fator entre tensão e corrente é de 10, pois 5V geram 0,5A. Esse comportamento pode ser melhor compreendido ao avaliar a curva U x I para diferentes valores de resistência. A inclinação da reta diminui conforme a resistência elétrica aumenta.

2° Lei de Ohm

A segunda lei de Ohm aborda o cálculo da resistência elétrica de resistores. De acordo com ela, a resistência é afetada por 3 parâmetros, sendo eles

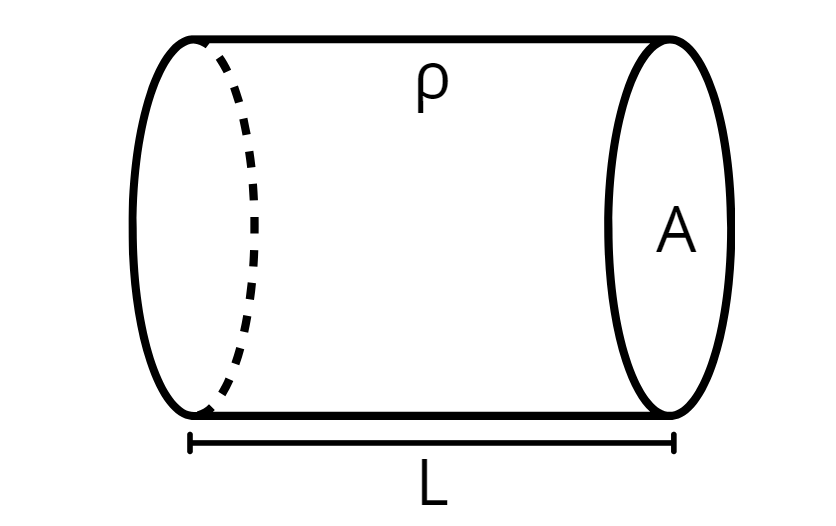
• Resistividade do Material (ρ) - É algo intrínseco do material da qual o resistor é fabricado. É medido em Ωm.

• Área Transversal (A) - É a área pela qual a corrente poderá passar. É medida em m².

• Comprimento (L) - É o comprimento do fio / resistor. É medido em metros (m).

A fórmula que descreve a resistência em função desses parâmetros é

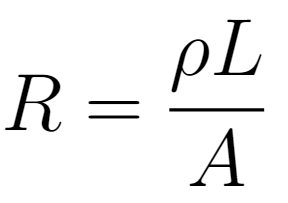
Potência Consumida

Utilizando a primeira lei de Ohm e sabendo que a potência consumida por um circuito elétrico é dada por

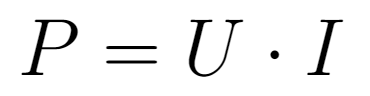
É possível obter as duas expressões abaixo para a potência consumida por uma resistência.

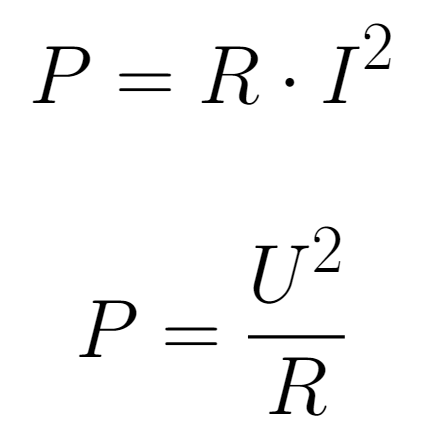
Resistores Reais

Os tipos mais comuns de resistores tem formato cilíndrico e apresentam algumas faixas coloridas. Essas faixas ajudam a identificar o valor da resistência elétrica e a sua precisão.

Os resistores tem 4 ou 5 faixas, e cada faixa tem uma função específica. A tabela abaixo mostra a função de cada faixa.

As duas primeiras faixas representam os dois primeiros dígitos da resistência. Uma terceira faixa pode ser adicionada em alguns casos para dar mais precisão, porém nem sempre aparece. Por exemplo, caso as três primeiras faixas forem Marrom, Preta e Preta, representaria o número 100.

A quarta faixa é utilizada como multiplicador. Esse valor deve ser multiplicado pelo valor dos 2/3 dígitos anteriores para obter a resistência completa. Pensando ainda no exemplo anterior, caso a quarta faixa fosse Amarela, teríamos 100 x 10k = 1MΩ.

A última faixa representa a tolerância do resistor, ou seja, seu erro máximo. Os valores mais comuns são 5% e 1%. Porém, em algumas aplicações onde a precisão é importante, é possível achar resistores com erros menores.

Cor	1° Faixa	2° Faixa	3° Faixa (opcional)	Multiplicador	Tolerância
Preto	0	0	0	1
Marrom	1	1	1	10	1%
Vermelho	2	2	2	100	2%
Laranja	3	3	3	1k
Amarelo	4	4	4	10k
Verde	5	5	5	100k	0,5%
Azul	6	6	6	1M	0,25%
Violeta	7	7	7	10M	0,1%
Cinza	8	8	8		0,05%
Branco	9	9	9
Dourado				0,1	5%
Prata				0,01	10%

Associação de Resistores

Associação em Série

É possível associar resistores em circuitos mais complexos, a fim de obter comportamentos desejados. No exemplo abaixo, temos resistores associados em série. A corrente passa por todos os resistores de uma vez, porém a tensão é dividida entre os três.

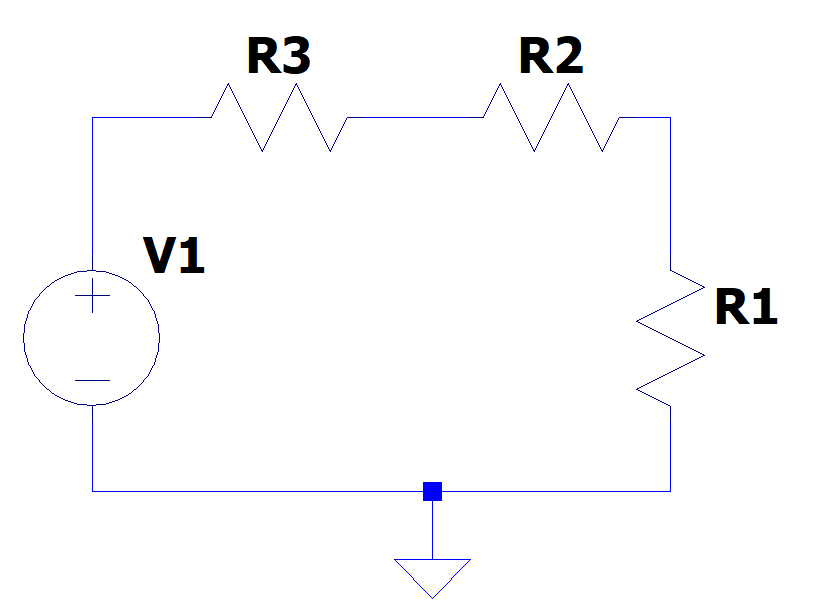
A resistência equivalente da associação de resistores nesse formato é dada por

Ou seja, ao associar resistores em série, a resistência equivalente aumentará. A corrente que passa pelo circuito é

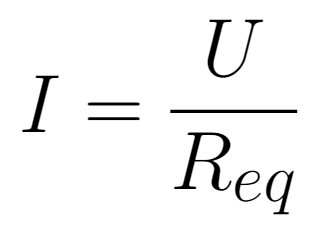
Já a tensão de cada componente não é a mesma. A tensão será dividida entre os resistores de modo que, quanto maior a resistência elétrica, maior a tensão. As equações para as tensões dos 3 resistores são

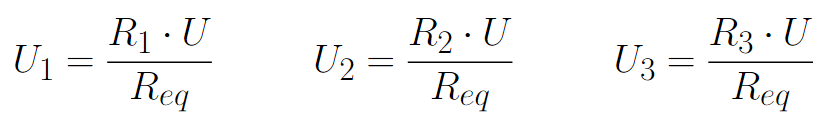
Associação em Paralelo

Ao associar resistores em paralelo, a tensão aplicada em todos é a mesma, porém a corrente não.

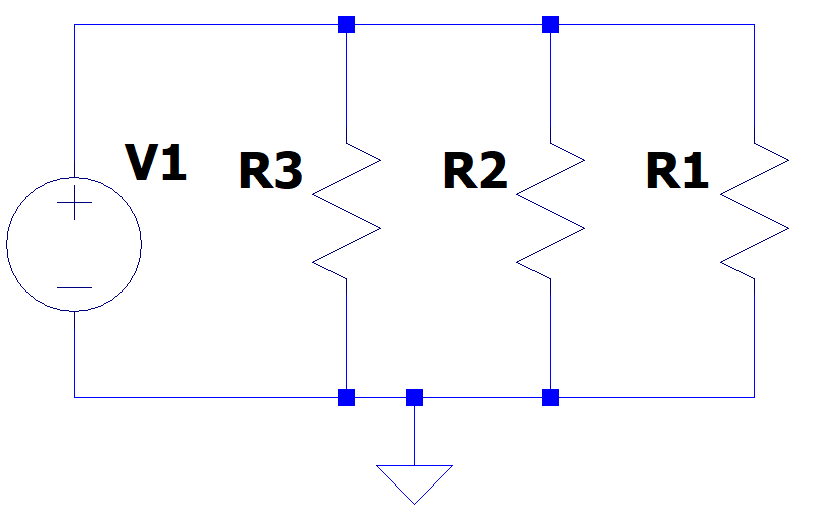
Esse tipo de associação pode ser pensado como se tivessem sido criados 3 caminhos para a passagem de corrente. Ou seja, adicionar mais resistores em paralelo vai fazer a resistência equivalente diminuir, pois mais rotas para a corrente vão ser criadas e, consequentemente, mais corrente passará pelo circuito. A fórmula para a resistência equivalente de associações em paralelo é

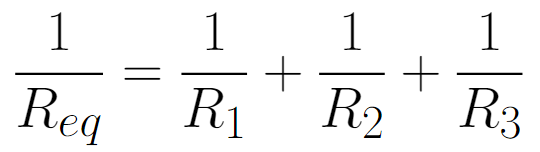
A corrente elétrica que passa por cada resistor pode ser calculada utilizando.

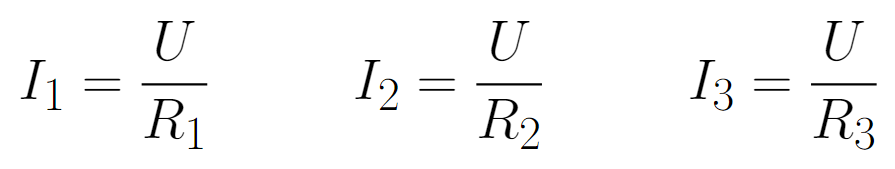
Conclusões

Em conclusão, os resistores desempenham um papel fundamental nos circuitos eletrônicos. Compreender os conceitos básicos relacionados aos resistores, como a resistência, a lei de Ohm e os tipos de resistores, é crucial para projetar e analisar circuitos de forma eficaz.

Ao dominar esses conceitos, é possível otimizar o desempenho e a segurança de sistemas elétricos, garantindo maior eficiência e confiabilidade. A importância dos resistores é incontestável, e seu estudo contínuo é essencial para a evolução das tecnologias eletrônicas.